Operaciones con Intervalos
En las matemáticas, podemos definir a un conjunto como una colección desordenada de objetos, los objetos de un conjunto pueden ser cualquier cosa siempre que tengan una relación entre ellos, a los objetos de un conjunto de les llama elementos o miembros de dicho conjunto, por lo tanto un conjunto contiene a sus elementos Se representan con una letra mayúscula y a los elementos o miembros de ese conjunto se les mete entre llaves ({,}).
· Dos conjuntos se pueden combinar de muchas maneras distintas, por ejemplo, teniendo un conjunto de la gente que juega al fútbol y otro de la gente que juega a baloncesto podemos hacer muchas combinaciones como el conjunto de personas que juegan a fútbol o baloncesto, las que juegan a fútbol y baloncesto, las que no juegan a baloncesto, etc.
Intervalos
Se pueden clasificar los intervalos según sus características topológicas: (intervalos abiertos, cerrados, semiabiertos) o según sus características métricas (longitud: nula, finita no nula, infinita). Intervalo semiabierto (cerrado en a, abierto en b). Intervalo semiabierto (abierto en a, cerrado en b).
OPERACIONES CON INTERVALOS
Dado que los intervalos constituyen un tipo particular de conjuntos, definiremos a continuación algunas operaciones, con conjuntos en general, e ilustraremos estas operaciones mediante ejemplos, de entre los cuales en algunos casos se involucraron intervalos.
1. INTERSECCION
Sean A y B conjuntos. Se define la intersección de A y B y se denota A ∩ B, al conjunto cuyos elementos pertenecen a A y también a B.
2. UNION
Sean A y B y conjuntos. Se define la unión de A y B y se denota A U B, al conjunto cuyos elementos pertenecen al menos a uno de los dos conjuntos A y B.











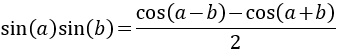








 Calculamos el seno y coseno del ángulo
Calculamos el seno y coseno del ángulo 


 , porque no puedo construir un triángulo rectángulo con un ángulo de 150°.
, porque no puedo construir un triángulo rectángulo con un ángulo de 150°.















 obtengo
obtengo obtendría
obtendría